Задача
Сколько существует натуральных чиселn, меньших 10000, для которых 2n–n² делится на 7?
Решение
Остатки от деления 2nна 7 повторяются с периодом 3: 2, 4, 1. Остатки от деленияn² на 7 повторяются с периодом 7: 1, 4, 2, 2, 4, 1, 0. Поэтому делимость на 7 зависит только от остатка при деленииnна 21. Рассмотрим все случаи (в первой строке таблицы – остатки от деления на 21, в следующих двух – остатки от деления на 7).
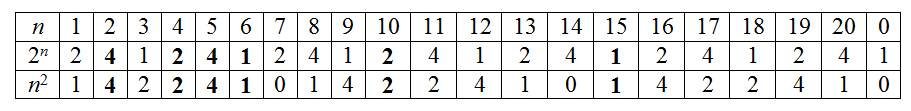
Ответ
2858 чисел.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет