Будем называть число N выигрышным, если при начале игры с него выигрывает первый, и проигрышным, если второй. Число является выигрышным тогда и только тогда, когда существует ход из него в проигрышное число, а проигрышным – тогда и только тогда, когда любой ход из него ведёт в выигрышное число.   Пользуясь этим утверждением, можно, рассматривая натуральные числа последовательно, выяснить про любое конкретное число, является оно выигрышным или проигрышным: число 1 – проигрышное, число 2 – выигрышное, число 3 – проигрышное (так как единственный ход ведет из него в выигрышное число 2), число 4 – выигрышное (так как из него есть ход в проигрышное число 3) и так далее:

  Заметим, что число 16 является проигрышным, а, следовательно, простое число 17 является выигрышным. Число 33 – выигрышное: из него можно пойти в проигрышное число 3. Поэтому число 34 является хоть и составным, но проигрышным (все три хода из него – в 2, в 17 и в 33 – ведут в выигрышные числа).   Докажем, что 2 и 17 – единственные выигрышные простые числа. Предположим, что это не так, и рассмотрим следующее выигрышное простое число p. В таком случае  p – 1  – проигрышное чётное число, поэтому среди делителей числа  p – 1  не может быть проигрышных простых чисел, то есть  p – 1 = 2ⁿ·17^k  (n ≥ 1).  Но тогда от него можно перейти либо к числу 34, либо к числу 16 и выиграть.   Если составное число N имеет простой делитель p, отличный от 2 и 17, то из него есть ход в проигрышное число p, то есть число N является выигрышным. Остались числа вида  N = 2ⁿ·17^k.

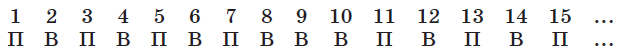
  Выше показано, что 2, 4, 8 – выигрышные, а 16 – проигрышное, поэтому числа 2ⁿ  (n > 4)  – выигрышные: от них можно перейти к 16.

  Число 34 – проигрышное; поэтому числа вида  N = 2ⁿ·17^k  (n, k > 1)  – выигрышные: от них можно перейти к 34.

  Число  17² = 289  – проигрышное; поэтому числа 17^k  (k > 2)  – выигрышные, от них можно перейти к 17².

При  N = 2,  N = 17,  а также при всех составных N, кроме  N = 16, 34 и 289.