Назад
Задача 132892 • Сложность: 2 • 8-9 класс
Задача

В треугольнике ABC, где угол B прямой, а угол A меньше угла C, проведена медиана BM. На стороне AC взята точка L так, что  ∠ABM = ∠MBL.  Описанная окружность треугольника BML пересекает сторону AB в точке N. Докажите, что  AN = BL.

Авторы:
Лопатников А. А.
Разделы:
Планиметрия
Источники:
Московская математическая олимпиада Олимпиады и турниры 2013 год
Количество версий:
4
Решение

  Так как BM – медиана в прямоугольном треугольнике, то треугольник AMB равнобедренный, поэтому  ∠MAN = ∠ABM = ∠MBL

(см. рис.).

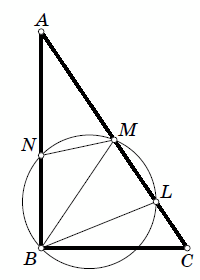
  Далее можно рассуждать по разному.   Первый способ. Из вписанности четырёхугольника BLMM следует, что  ∠MNA = ∠MLB.  Таким образом, треугольники AMN и BML равны по двум углам и стороне. Значит,  AN = BL.   Второй способ. Углы NBM и NLM опираются на одну дугу, поэтому  ∠NLM = ∠NBM = ∠NAL.  Значит, треугольник ANL равнобедренный,  AN = LN,  а  ∠BNL = 2∠BAM = 2∠NBM = ∠NBL.  Поэтому треугольник NLB равнобедренный, то есть BL = NL = AN.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет