Задача
Известно, что x + 2y + 3z = 1. Какое минимальное значение может принимать выражение x² + y² + z²?
Решение
Рассмотрим прямоугольную систему координат в пространстве. Проведем плоскость П, заданную уравнением x + 2y + 3z = 1. Выражение
x² + y² + z² равно квадрату расстояния от начала координат O до точки с координатами (x, y, z). Расстояние от начала координат до точки
(x, y, z), лежащей в плоскости П, не превосходит расстояния от начала координат до плоскости П. Поэтому минимальное значение выражения x² + y² + z² при условии x + 2y + 3z = 1 достигается тогда, когда точка (x, y, z) является основанием перпендикуляра, опущенного из O на плоскость П, и равно квадрату расстояния от O до плоскости П. Это расстояние можно вычислить по известной формуле. В результате получим 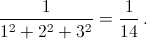
Ответ
1/14.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь