Пусть B1— точка пересечения биссектрисы треугольника ABC , проведённой из вершины B , с описанной окружностью (рис.1). Обозначим 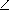ABC = β , 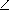ACB = γ . По теореме о внешнем угле треугольника

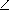B1O1C = 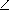O1BC + 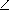O1CB = +.

С другой стороны,

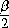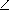O1CB1 = 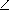O1CA+ 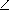B1C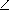A = O1CA+ 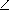B1BA = +.

Значит, треугольник O1B1C — равнобедренный. По теореме об отрезках пересекающихся хорд

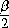B1O1· O1B = (R + O1O2)(R - O1O2) = R2 - O1O22.

Пусть P — проекция точки O1на сторону BC . Тогда O1P=r . Из прямоугольного треугольника BO1P находим, что

O1B = = ,

а т.к.

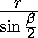B1O1 = B1C = 2R sin 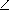B1BC = 2R sin ,

то

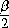R2 - O1O22 = 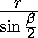· 2R sin = 2rR.

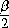Следовательно, O1O22 = R2 - 2rR .

Пусть вписанная окружность касается сторон AB , AC и BC треугольника ABC в точках C' , B' и A' соответственно (рис.2). При инверсии относительно окружности с центром O1, вписанной в треугольник ABC , вписанная окружность останется на месте, прямые, содержащие стороны треугольника перейдут в окружности, проходящие через центр O1инверсии и касающиеся окружности инверсии, поэтому вершины A , B и C перейдут в середины отрезков B'C' , A'C' и B'C' соответственно. Тогда окружность, с центром O2, описанная около треугольника ABC , перейдёт в окружность с центром O радиуса , проходящую через середины сторон треугольника A'B'C' . Эта окружность гомотетична описанной окружности треугольника ABC , причём центр гомотетии совпадает с центром O1инверсии, значит, точка O лежит на прямой O1O2. Пусть O1O2=d , XY — диаметр описанной окружности треугольника ABC , проходящий через точку O1, а M и N — образы точек соответственно X и Y при рассматриваемой инверсии (рис.3). Тогда

MN=XY· = 2R· =,

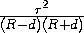а т.к. MN = r , то =r . Отсюда находим, что d2=R2-2rR .

Ответ задачи отсутствует