Задача
Докажите, что если четырёхугольник вписан в окружность, то сумма произведений длин двух пар его противоположных сторон равна произведению длин его диагоналей.
Решение
Пусть четырёхугольник ABCD вписан в окружность. Первый способ. Рассмотрим на диагонали AC такую точку P, что ∠ABP = ∠CBD (рис. слева).
Треугольники ABP и DBC подобны по двум углам. Поэтому ∠AB : AP = BD : CD, то есть AB·CD = AP·BD.
Поскольку ∠ABD = ∠ABP + ∠PBD = ∠CBD + ∠PBD = ∠PBC, треугольники PBC и ABD также подобны по двум углам. Поэтому BC·AD = PC·BD.
Сложив почленно эти равенства, получим, что AB·CD + BC·AD = AP·BD + BD·PC = BD·(AP + PC) = BD·AC.
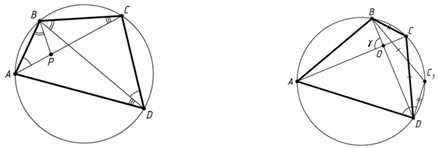
Пусть C1 – точка, симметричная вершине C относительно серединного перпендикуляра к отрезку BD. Тогда точка C1 также лежит на окружности, четырёхугольники ABCD и ABC1D равновелики, BC1 = DC, DC1 = BC, а ∠ADC1 = ½ (⌣AB + ⌣CD) = γ.
Значит, SABCD = SABC1D = SADC1 + SABC1 = AD·DC1 sin γ + AB·BC1 sin(180° − γ) = (AD·BC + AB·CD) sin γ. Таким образом, AC·BD sin γ = (AD·BC + AB·CD) sin γ, то есть AC·BD = AD·BC + AB·CD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь