Радиус окружности, касающейся гипотенузы и катетов — задача по планиме
Задача
Пусть r — радиус окружности, касающейся гипотенузы и продолжения катетов прямоугольного треугольника со сторонами a, b, c. Докажите, что r = ${\frac{a+b+c}{2}}$.
Решение
Обозначим вершины треугольника, противолежащие сторонам a, b, c, через A, B, C (C — вершина прямого угла), а точки касания — через A1, B1, C1 соответственно. Если O — центр данной окружности, то OA1CB1 — квадрат со стороной, равной r. Поэтому
CA1 = r, BC1 = BA1 = r - a, AC1 = AB1 = r - b,
c = AB = AC1 + C1B = 2r - a - b.
Следовательно,r=${\frac{a+b+c}{2}}$.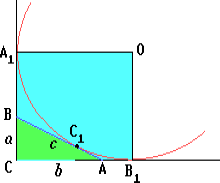
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет