Расстояние от вершины треугольника до точки касания окружности
Задача
В треугольник ABC вписана окружность. Пусть x — расстояние от вершины A до касания окружности со стороной AB, BC = a. Докажите, что x = p - a, где p — полупериметр треугольника.
Решение
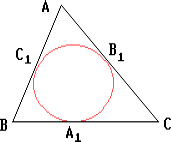
Обозначим точки касания вписанной окружности со сторонами AB, BC и AC через C1, A1 и B1 соответственно. Пусть AC = b и AB = c. Тогда
BA1 = BC1 = AB - AC1 = c - x, CA1 = CB1 = AC - AB1 = b - x,
BC = BA1 + CA1 = c - x + b - x = b + c - 2x.
Следовательно,
x = $\displaystyle {\frac{b + c - a}{2}}$ = $\displaystyle {\frac{b + c + a}{2}}$ - a = p - a.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет