Задача
Докажите, что прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним.
Решение
Пусть A и B — точки пересечения двух окружностей, MN — общая касательная (M и N — точки касания), K — точка пересечения прямых AB и MN (A между K и B). Тогда
MK2 = KB . KA и NK2 = KB . KA.
Следовательно,MK=NK.
Пусть A и B — точки пересечения двух окружностей, MN — общая
касательная (M и N — точки касания), K — точка пересечения прямых
AB и MN (A между K и B). Тогда
MK2 = KB . KA и NK2 = KB . KA.
Следовательно,MK=NK.
Пусть A и B — точки пересечения двух окружностей, MN — общая
касательная (M и N — точки касания), K — точка пересечения прямых
AB и MN (A между K и B). Тогда
MK2 = KB . KA и NK2 = KB . KA.
Следовательно,MK=NK.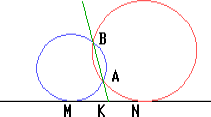
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет