Олимпиадная задача: площадь треугольника через полупериметр и радиус
Задача
Докажите, что площадь треугольника равна его полупериметру, умноженному на радиус вписанной окружности.
Решение
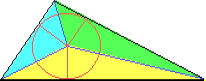
Соединим центр O вписанной окружности радиуса r треугольника ABC с вершинами треугольника. Пусть BC = a, AC = b, AB = c. Тогда
S$\scriptstyle \Delta$ABC = S$\scriptstyle \Delta$BOC + S$\scriptstyle \Delta$AOC + S$\scriptstyle \Delta$AOB =
= $\displaystyle {\textstyle\frac{1}{2}}$ar + $\displaystyle {\textstyle\frac{1}{2}}$br + $\displaystyle {\textstyle\frac{1}{2}}$cr = $\displaystyle {\frac{a+b+c}{2}}$r = pr,
гдеp— полупериметр треугольника.
Аналогичная формула верна для площади любого описанного
многоугольника.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет