Задача по олимпиадной математике: перпендикулярность прямых в треуголь
Задача
В треугольнике ABC проведены высоты BB1 и AA1; O — центр описанной около треугольника ABC окружности. Докажите, что прямые
A1B1 и CO перпендикулярны.
Решение
Первый способ.
Пусть треугольник ABC — остроугольный и
$\angle$CAB = $\alpha$. Тогда
$\displaystyle \angle$CA1B1 = $\displaystyle \alpha$, $\displaystyle \angle$COB = 2$\displaystyle \alpha$, $\displaystyle \angle$OCB = 90o - $\displaystyle \alpha$.
Поэтому
$\displaystyle \angle$OCB + $\displaystyle \angle$B1A1C = $\displaystyle \alpha$ + 90o - $\displaystyle \alpha$ = 90o.
Для тупоугольного треугольника доказательство аналогично.
Второй способ.
Треугольник
A1CB1 подобен треугольнику ACB. Пусть CC1 —
высота треугольника ACB. Поскольку
$\angle$OCB = $\angle$ACC1, то высота CP
треугольника
A1CB1 лежит на прямой CO.
Третий способ.
Проведём касательную CK к описанной окружности треугольника ABC (точки K и A лежат
по разные стороны от прямой BC). Из теоремы об угле между касательной и хордой
следует, что
$\displaystyle \angle$BCK = $\displaystyle \angle$BAC = $\displaystyle \angle$CA1B1.
Значит,CK||A1B1, а т.к.OC$\perp$CK, тоOC$\perp$A1B1.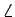
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет