Задача
Докажите, что высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника (т.е. треугольника с вершинами в основаниях высот данного).
Решение
Пусть A1, B1 и C1 — основания высот остроугольного треугольника ABC, проведённых из вершин A, B и C соответственно. Тогда
$\displaystyle \angle$AC1B1 = $\displaystyle \angle$ACB, $\displaystyle \angle$BC1A1 = $\displaystyle \angle$ACB.
Поэтому
$\displaystyle \angle$AC1B1 = $\displaystyle \angle$BC1A1.
Следовательно,
$\displaystyle \angle$B1C1C = 90o - $\displaystyle \angle$AC1B1 = 90o - $\displaystyle \angle$BC1A1 = $\displaystyle \angle$A1C1C.
Аналогично
$\displaystyle \angle$A1B1B = $\displaystyle \angle$C1B1B, $\displaystyle \angle$B1A1A = $\displaystyle \angle$C1A1A.
Если треугольник тупоугольный, то две его высоты — биссектрисы внешних углов
ортотреугольника, а третья — биссектриса внутреннего угла.
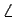
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет