Задача
Докажите, что сумма квадратов расстояний от точки, лежащей на окружности, до вершин правильного вписанного в эту окружность треугольника есть величина постоянная, не зависящая от положения точки на окружности.
Решение
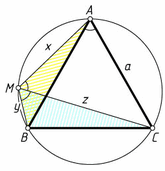
Пусть M – произвольная точка меньшей дуги AB описанной окружности равностороннего треугольника ABC. Обозначим AM = x, CM = z, BM = y, AB = BC = AC = a. Тогда ∠AMC = ∠BMC = 60°, а согласно задаче 52355 z = x + y.
Применив теорему косинусов к треугольникам AMC и BMC, получим 2a² = a² + a² = (x² + z² – xz) + (y² + z² – yz) = x² + y² + 2z² – (x + y)z = x² + y² + z².
Таким образом, сумма квадратов расстояний от любой точки окружности до вершин треугольника равна 2a².
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь