Олимпиадная задача по планиметрии: равнобедренность треугольников MBQ
Задача
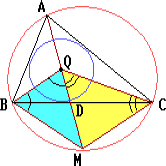
Продолжение биссектрисыADтреугольникаABCпересекает описанную окружность в точкеM. ПустьQ- центр окружности, вписанной в треугольникABC. Докажите, что треугольникиMBQиMCQ- равнобедренные.
Решение
Обозначим$\angle$A=$\alpha$,$\angle$B=$\beta$. Тогда
$\displaystyle \angle$BQM = $\displaystyle \angle$ABQ + $\displaystyle \angle$BAQ = $\displaystyle \alpha$/2 + $\displaystyle \beta$/2,
$\displaystyle \angle$QBM = $\displaystyle \angle$QBD + $\displaystyle \angle$DBM = $\displaystyle \angle$QBD + $\displaystyle \angle$MAC = $\displaystyle \beta$/2 + $\displaystyle \alpha$/2.
Следовательно,$\angle$BQM=$\angle$QBM.
Аналогично
$\angle$MCQ = $\angle$MQC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет