Задача
Докажите, что точка пересечения диагоналей описанного вокруг окружности четырёхугольника совпадает с точкой пересечения диагоналей четырёхугольника, вершинами которого служат точки касания сторон первого четырёхугольника с окружностью.
Решение
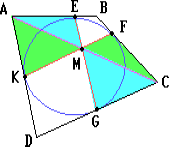
Пусть E, F, G и K — точки касания окружности со сторонами AB, BC, CD и AD описанного четырёхугольника ABCD, M — точка пересечения AC и EG. Тогда
$\displaystyle {\frac{S_{\Delta AEM}}{S_{\Delta CGM}}}$ = $\displaystyle {\frac{AM\cdot EM \sin \angle AME}{CM\cdot GM \sin \angle CMG}}$ = $\displaystyle {\frac{AE\cdot EM\sin \angle AEM}{CG\cdot GM\sin \angle CGM}}$.
Посколькуsin$\angle$AME= sin$\angle$CMGиsin$\angle$AEM= sin$\angle$CGM,
то из полученного равенства отношений следует, что${\frac{AM}{CM}}$=${\frac{AE}{CG}}$, т.е.
прямаяEGделит диагональACданного четырёхугольника в отношении${\frac{AE}{CG}}$.
Точно так же убеждаемся, что прямая FK делит ту же диагональ
в отношении
${\frac{AK}{CF}}$, а т.к. AE = AK и CG = CF,
то
${\frac{AK}{CF}}$ = ${\frac{AE}{CG}}$.
Следовательно, прямая FK проходит через точку M.
Аналогично докажем, что BD проходит через точку пересечения EG и FK.
Это утверждение можно доказать с помощью теоремы Брианшона (см. Г.С.М.Коксетер, С.Л.Грейтцер: Новые встречи с геометрией, с.98).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет