Задача
Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию. Верно ли обратное?
Решение
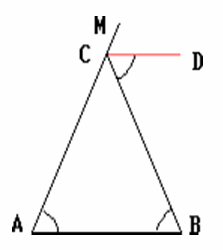
Пусть CD – биссектриса угла BCM, смежного с углом при вершине C равнобедренного треугольника ABC (см. рис.). Тогда ∠BCM = ∠A + ∠B = 2∠B, а ∠BCD = ½ ∠BCM = ∠B.
Углы BCD и ABC – накрест лежащие при прямых AB и CD и секущей CB. Поскольку они равны, то прямые AB и CD параллельны.
Ответ
Верно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет