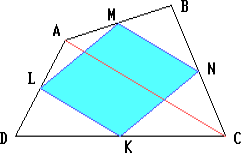
Пусть M, N, K, L — середины сторон соответственно AB, BC, CD, AD четырёхугольника ABCD. Поскольку MN — средняя линия треугольника ABC, то MN = ${\frac{{1}}{{2}}}$AC и MN$\Vert$AC. Аналогично докажем, что

KL = ${\frac{{1}}{{2}}}$AC и KL$\Vert$AC. Значит, MN = KL и MN$\Vert$KL. Следовательно, четырёхугольник MNKL — параллелограмм.

Ответ задачи отсутствует