Длина отрезка между серединами диагоналей трапеции — олимпиадная задач
Задача
Основания трапеции равны a и b (a > b). Найдите длину отрезка, соединяющего середины диагоналей трапеции.
Решение
Пусть M и N – середины диагоналей AC и BD трапеции ABCD, в которой AD = a и BC = b.
Соединим точку M с серединой K боковой стороны CD. По теореме о средней линии треугольника MK || AD || BC. Аналогично, NK || BC.
Следовательно, точки M, N и K лежат на средней линии трапеции. Таким образом, MN = MK – KN = ½ AD – ½ BC = ½ (a – b). 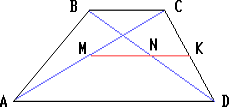
Ответ
½ (a – b).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет