Задача
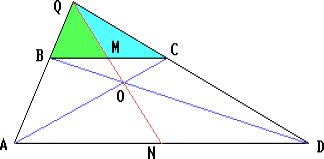
Докажите, что точка пересечения продолжений боковых сторон трапеции, середины оснований и точка пересечения диагоналей лежат на одной прямой.
Решение
При гомотетии с центром в точке O пересечения диагоналей AC и BD, переводящей вершину B трапеции ABCD в вершину D, точка C переходит в точку A, основание BC – в основание DA, середина M основания BC – в середину N основания DA. Следовательно, прямая MN проходит через центр гомотетии, то есть через точку O.
Аналогично доказывается, что прямая MN проходит через точку пересечения прямых AB и DC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет