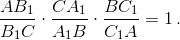
Решение 1:   Необходимость. Пусть отрезки AA₁, BB₁ и CC₁ пересекаются в точке M.   Первый способ. Проведём через вершину B прямую, параллельную AC, и продолжим отрезки AA₁ и CC₁ до пересечения с этой прямой в точках K и N соответственно (см. рис.).

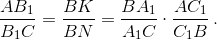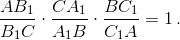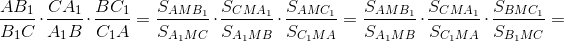
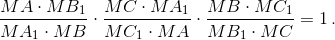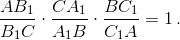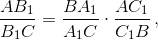  Из подобия треугольниковBA₁KиCA₁Aследует, что  BK = AC·^BA₁/_A1C.  Аналогично  BN = AC·^BC₁/_C1A.  Кроме того,  ^AB₁/_BK=^B₁M/_MB=^CB₁/_BN.  Следовательно,    Поэтому     Второй способ.       Достаточность. Пусть     Предположим, что прямая, проходящая через вершину B и точку пересечения отрезков AA₁ и CC₁, пересекает сторону AC в точке P. Тогда по доказанному     а так как по условию     то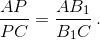  

  Следовательно, точки P и B совпадают.

Решение 2:   Пусть прямые AA₁ и CC₁ пересекаются в точке M. Обозначим  ^AC₁/_C1B = p,  ^BA₁/_A1C = q.  Нужно доказать, что прямая BB₁ проходит через точку M тогда и только тогда, когда  CB₁ : B₁A = 1 : pq.

  Поместим в точки A, B и C массы 1, p и q соответственно. Тогда C₁ – центр масс точек A и B, а A₁ – центр масс точек B и C. Центр масс точек A, B и C с данными массами лежит и на отрезке AA₁ и и на отрезке CC₁, то есть совпадает с M.

  С другой стороны, точка M лежит на отрезке, соединяющем точку B с центром масс точек A и C, то есть с точкой, лежащей на стороне AC и делящей её в отношении  CB₁ : B₁A = 1 : pq.

  Остаётся заметить, что на отрезке AC существует единственная точка, делящая его в данном отношении.

Ответ задачи отсутствует