Задача
Дан треугольник ABC. Некоторая прямая пересекает его стороны AB, BC и продолжение стороны AC в точках C1, A1, B1 соответственно. Докажите, что
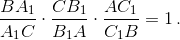
Решение
Решение 1: Через вершину B проведём прямую, параллельную AC. Пусть K – точка её пересечения с прямой B1C1 (рис. слева).
Из подобия треугольников BC1K и
AC1B1 следует, что
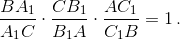Из подобия треугольников BA1K и CA1B1 следует, что 
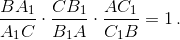Поэтому 
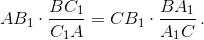Следовательно,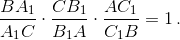 
Решение 2: Пусть l – произвольная прямая, пересекающая прямую A1C1 в точке L. Через точки A, B и C проведём прямые, параллельные прямой A1C1. Пусть A2, B2, C2 – точки пересечения этих прямых с прямой l (рис. справа). По теореме о пропорциональных отрезках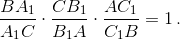 
Следовательно, 
Решение 3: Пусть a, b, c – длины высот треугольников
AB1C1, BA1C1, CA1B1, проведённых из вершин A, B, C соответственно. Тогда 
Следовательно,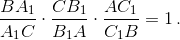
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь