Задача
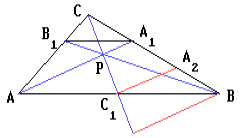
Через точку P, лежащую на медиане CC1 треугольника ABC, проведены прямые AA1 и BB1 (точки A1 и B1 лежат на сторонах BC и CA соответственно).
Докажите, что A1B1 || AB.
Решение
Пусть $A_2$ – середина отрезка $A_1B$. Тогда $C_1A_2$ – средняя линия треугольника $ABA_1$, и, следовательно, $A_1P || C_1A_2$. Тогда из теоремы Фалеса $CA_1 : A_1A_2 = CP : PC_1$, и, поскольку $A_1B = 2A_1A_2$, справедливо $CA_1 : A_1B = CP : 2 PC_1$. Аналогично, $CB_1 : B_1A = CP : 2 PC_1.$ Поэтому $CB_1 : B_1A = CA_1 : A_1B$. Следовательно, $A_1B_1 || AB$.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет