Первый способ. Предположим, что нужный треугольник ABC построен. Пусть  BC = a  и  AC = b  – его данные стороны, CM – медиана,  ∠ACM = α,

∠BCM = 2α.  Если E – точка, симметричная вершине B относительно прямой CM, то  CE = CB = a,  ∠ECM = ∠BCM = 2α,  ∠ECA = α.  Поскольку

ME = MB = MA,  то  ∠AEB = 90°.  Поэтому  AE || EC,  ∠EAC = ∠MCA = α.  Следовательно, треугольник AEC равнобедренный, то есть  AE = EC = a.

  Отсюда вытекает следующее построение. Строим равнобедренный треугольник ACE по трём сторонам. Через вершину C проводим прямую, параллельную AE. Образ точки E при симметрии относительно этой прямой есть искомая вершина B. 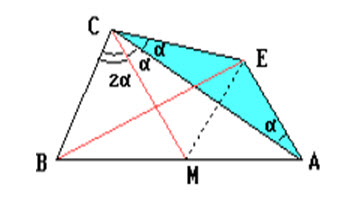  Второй способ. Применив теорему синусов к треугольникам BCM и ACM, находим, что  a sin 2α = b sin α.  Поэтому  cos α = ^b/_2a.  Следовательно, угол α можно построить.    Поскольку  0 < 3α < 180°,  то  0 < α < 60°.  Поэтому задача имеет решение (и притом единственное) при  a < b.

Ответ задачи отсутствует