Назад
Задача 154742 • Сложность: 2 • 8-9 класс
Задача

На прямой выбрали четыре точки A, B, C, D и измерили расстояния AB, AC, AD, BC, BD и CD. Могут ли они быть равными (в порядке возрастания)

  а) 1, 2, 3, 4, 5, 6;

  б) 1, 1, 1, 2, 2, 4.

Разделы:
Планиметрия
Источники:
Система задач по геометрии Р.К.Гордина (zadachi.mccme.ru) Интернет-ресурсы
Количество версий:
4
Решение

а) Пример:

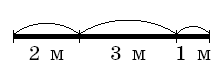
б) Расстояния между несоседними точками не могут равняться 1 (как сумма двух или трёх натуральных чисел). Значит, все три расстояния между сосодями равны 1. Но тогда расстояние между крайними точками равно 3, а оно наибольшее и должно равняться 4. Противоречие.
Ответ

а) Могут;  б) не могут.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет