Задача
Докажите. что если в трапеции ABCD середину M одной боковой стороны AB соединить с концами другой боковой стороны CD, то площадь полученного треугольника CMD составит половину площади трапеции.
Решение
Пусть высота данной трапеции равна h. Тогда высоты треугольников MBC и MAD, проведённые из вершины M, равны ${\frac{h}{2}}$. Сумма площадей этих треугольников равна
$\displaystyle {\textstyle\frac{1}{2}}$ . $\displaystyle {\textstyle\frac{1}{2}}$h . BC + $\displaystyle {\textstyle\frac{1}{2}}$ . $\displaystyle {\textstyle\frac{1}{2}}$ . h . AD = $\displaystyle {\textstyle\frac{1}{4}}$(BC + AD)h,
т.е. половине площади трапеции.
Поэтому и площадь треугольникаCMDравна половине площади
трапеции.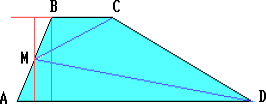
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет