Задание олимпиады: две прямые и деление сторон четырёхугольника
Задача
Две прямые делят каждую из двух противоположных сторон выпуклого четырёхугольника на три равные части.
Докажите, что между этими прямыми заключена треть площади четырёхугольника.
Решение
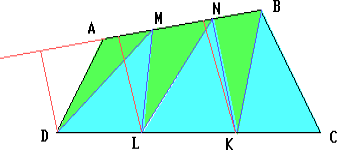
Пусть точки M и N лежат на стороне AB выпуклого четырёхугольника ABCD, точки K и L – на стороне DC, причём AM = MN = NB, DL = LK = KC.
Проведём диагонали DM, LN и KB четырёхугольников AMLD, MNKL и NBCK. Пусть h1, h и h2 – расстояния от точек соответственно D, L и K до прямой AB. Тогда h = ½ (h1 + h2) (h – длина средней линии трапеции с основаниями длины h1 и h2).
Поэтому SKLN = ½ MN·h = ¼ MN·(h1 + h1) = ¼ (AM·h1 + NB·h2) = ½ (SAMD + SCBK).
Аналогично, SKLM = ½ (SDLM + SCKB). Поэтому SMNKL = ½ (SAMLD + SNBCK). Следовательно, SMNKL = 1/3 SABCD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь