Задача
Точка внутри правильного 2n-угольника соединена с вершинами. Возникшие 2nтреугольников раскрашены попеременно в голубой и красный цвет. Докажите, что сумма площадей голубых треугольников равна сумме площадей красных а) для n= 4, б) для n= 3, в) для произвольногоn.
Решение
Поскольку в правильном многоугольнике все стороны равны, достаточно доказать, что сумма высот красных треугольников равна сумме высот голубых.
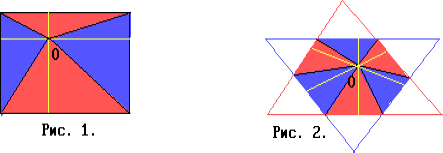
Если n чётно, то к противоположным сторонам 2n-угольника примыкают треугольники одного цвета, а сумма высот таких треугольников равна расстоянию между этими сторонами (рис. 1). Разбивая треугольники на пары, прилегающие к противоположным сторонам, получим утверждение задачи.
При нечётном n, продолжив "красные" стороны 2n-угольника, получим правильный n-угольник (рис. 2). Построенный таким же образом голубой n-угольник равен красному. Площадь голубого
n-угольника равна сумме высот голубых треугольников, умноженной на половину его стороны. То же верно и для красного n-угольника. Отсюда следует равенство сумм высот голубых и красных треугольников.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь