Задача
Отрезок соединяет вершину треугольника с точкой, лежащей на противоположной стороне. Докажите, что этот отрезок меньше большей из двух других сторон.
Решение
Первый способ.
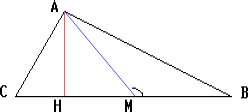
Пусть проекция H точки A на прямую BC принадлежит стороне
BC треугольника ABC. Если точка M лежит между точками H и C, то
HC > HM. Поэтому AM < AC.
Если M лежит между точками B и H, то BH > MH. Поэтому AM < AB.
Если M и H совпадают, то AM = AH < AC.
Аналогично рассматривается случай, когда точка H лежит на продолжении стороны BC.
Второй способ.
Если AM — высота треугольника ABC, то утверждение очевидно.
Предположим теперь, что AM не высота. Тогда один из углов AMB
или AMC — тупой. Пусть это угол AMB. Тогда в треугольнике AMB
сторона AB — наибольшая, т.к. она лежит против наибольшего
угла. Аналогично рассматривается второй случай.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет