Медиана треугольника ABC меньше полусуммы сторон — задание по олимпиад
Задача
Докажите, что медиана треугольника ABC, проведённая из вершины A, меньше полусуммы сторон AB и AC.
Решение
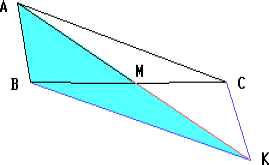
Отложим на продолжении медианы AM за точку M отрезок MK, равный AM. Тогда ABKC — параллелограмм. Применяя неравенство треугольника к треугольнику ABK, получим, что
2AM = AK < AB + BK = AB + AC.
Отсюда следует, что
AM < $\displaystyle {\frac{AB + AC}{2}}$.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет