Пусть M – точка пересечения диагоналей AC и BD четырёхугольника ABCD. Применим неравенство треугольника к треугольникам ABC, ADC, BAD и BCD:   AC < AB + BC,  AC < DA + DC,  BD < AB + AD,  BD < CB + CD.  Сложив эти четыре неравенства, получим:  2(AC + BD) < 2(AB + BC + CD + A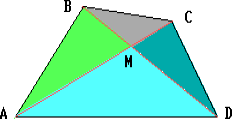D).   Запишем неравенства треугольника для треугольников AMB, BMC, CMD и AMD:  AM + MB > AB,  BM + MC > BC,  MC + MD > CD,  MA + MD > AD.  Сложив эти неравенства, получим:  2(AC + BD) > AB + BC + CD + AD.

Ответ задачи отсутствует