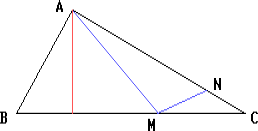
Сначала докажем, что отрезок AM, соединяющий вершину треугольника ABC, с точкой M, принадлежащей стороне BC, меньше большей из сторон AB и AC. Действительно, один из углов AMC и AMB — прямой или тупой. Тогда либо AM < AC, либо AM < AB. Отсюда следует требуемое утверждение.

Пусть теперь N — точка на стороне AC. Тогда MN меньше наибольшего из отрезков AM и MC. Кроме того, MC < BC, а AM меньше наибольшего из отрезков AB и AC. Следовательно, MN меньше наибольшей из сторон треугольника ABC.

Из доказанного утверждения следует, что диаметр треугольника (наибольшее из расстояний между точками, принадлежащими треугольнику) равен его наибольшей стороне.

Ответ задачи отсутствует