Задача
Пусть ABCD – выпуклый четырехугольник. Докажите, что AB + CD < AC + BD.
Решение
Пусть M – точка пересечения диагоналей данного четырёхугольника. Тогда AB < AM + BM, CD < CM + DM.
Сложив эти неравенства, получим AB + CD < AM + BM + CM + DM = (AM + CM) + (BM + DM) = AC + BD. 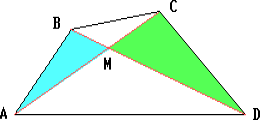
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет