Задача
Докажите, что в любом треугольнике большей стороне соответствует меньшая биссектриса.
Решение
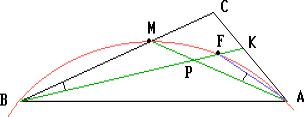
Пусть P — точка пересечения биссектрис AM и BK треугольника ABC, BC > AC. Обозначим
$\displaystyle \angle$ABC = $\displaystyle \beta$, $\displaystyle \angle$CAB = $\displaystyle \alpha$, $\displaystyle \angle$ACB = $\displaystyle \gamma$.
Тогда$\alpha$>$\beta$.
Отложим от луча AM в полуплоскости, содержащей точку C, луч
по углом
${\frac{\beta}{2}}$. Пусть F — точка пересечения этого луча
с биссектрисой BK. Отрезок MF виден из точек B и A под одним и
тем же углом
${\frac{\beta}{2}}$.
Следовательно, точки B, M, F и A лежат на одной окружности.
Кроме того,
$\angle$ABM = $\beta$ < 90o (т.к.
$\beta$ < $\alpha$)
и
$\displaystyle \angle$FAB = $\displaystyle {\frac{\alpha}{2}}$ + $\displaystyle {\frac{\beta}{2}}$ < $\displaystyle {\frac{\alpha}{2}}$ + $\displaystyle {\frac{\beta}{2}}$ + $\displaystyle {\frac{\gamma}{2}}$ = 90o.
Острые вписанные углыABMиFABопираются на хордыAMиBF,
и$\angle$FAB>$\angle$ABM. ПоэтомуBF>AM.
Следовательно,
BK = BF + FK > BF > AM.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет