Задача
Докажите, что если в выпуклом четырёхугольнике ABCD имеет место неравенство AB $\geqslant$ AC, то BD > DC.
Решение
Первый способ.
Пусть M — точка пересечения диагоналей AC и BD
данного четырёхугольника. Применим неравенство треугольника к
треугольникам AMB и DMC:
AM + BM > AB, DM + MC > DC.
Сложив почленно эти неравенства, получим, что
AC + BD > AB + DC.
ЕслиAB$\geqslant$AC, тоBD>DC.
Второй способ.
Рассмотрим треугольник ABC. В нём
AB $\geqslant$ AC, поэтому
$\angle$ACB $\geqslant$ $\angle$ABC. Поскольку луч CA проходит между
сторонами угла BCD, то
$\displaystyle \angle$DCB = $\displaystyle \angle$DCA + $\displaystyle \angle$ACB > $\displaystyle \angle$ACB $\displaystyle \geqslant$ $\displaystyle \angle$ABC = $\displaystyle \angle$DBC + $\displaystyle \angle$ABD > $\displaystyle \angle$DBC,
т.е. в треугольникеDBC$\angle$DCB>$\angle$DBC.
Следовательно,BD>DC.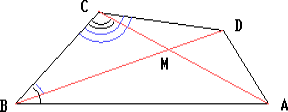
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет