Задача
Стороны треугольника равны a, b, c. Докажите, что медиана, проведённая к стороне c, равна ${\frac{1}{2}}$$\sqrt{2a^{2}+2b^{2}-c^{2}}$.
Решение
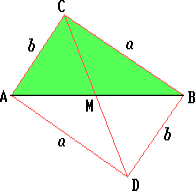
Пусть AB = c, BC = a, AC = b — стороны треугольника ABC; CM = m — медиана треугольника.
На продолжении медианы CM за точку M отложим отрезок MD, равный CM. Тогда ACBD — параллелограмм. Поэтому
CD2 + AB2 = 2(AC2 + BC2), или 4m2 + c2 = 2(a2 + b2).
Отсюда находим, что
m2 = $\displaystyle {\textstyle\frac{1}{4}}$(2a2 + 2b2 - c2).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет