Задача
Пусть H — точка пересечения высот треугольника ABC , O —
центр описанной окружности. Докажите, что 
=
+ 
+ 
.
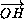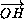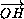Решение
Рассмотрим сумму векторов + =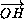 
.
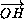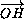Отрезок OK — диагональ ромба OAKB . Поэтому OK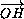 
AB .
Следовательно, OK || CH .
Тогда, если + =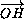
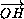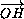, то точка M принадлежит высоте, проходящей через вершину C .
Таким образом, если + + =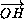
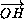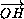1, то точка H1принадлежит каждой высоте треугольника ABC . Следовательно, точки H1и H совпадают.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет