Задачи и олимпиады по математике

Задача

Продолжение биссектрисы угла B треугольника ABC пересекает описанную окружность в точке M; O — центр вписанной окружности, O₁ — центр вневписанной окружности, касающейся стороны AC. Докажите, что точки A, C, O и O₁ лежат на окружности с центром в точке M.

Решение

Поскольку

$\displaystyle \angle$AOM = $\displaystyle \angle$ABO + $\displaystyle \angle$OAB = $\displaystyle \angle$ACM + $\displaystyle \angle$OAB =

= $\displaystyle \angle$CAM + $\displaystyle \angle$OAC = $\displaystyle \angle$OAM,

то треугольникOMA— равнобедренный,MO=MA. Аналогично докажем, чтоMO=MC. Угол OMO₁ — прямой как угол между биссектрисами смежных углов. Обозначим $\angle$AOM = $\angle$OAM = $\varphi$. Тогда

$\displaystyle \angle$MAO₁ = 90^o - $\displaystyle \varphi$, $\displaystyle \angle$MO₁A = 90^o - $\displaystyle \varphi$.

Поэтому треугольникAMO₁— равнобедренный иMA=MO₁. Следовательно,MA=MO=MC=MO₁. Поэтому точкиA,O,C,O₁лежат на окружности с центром в точкеM.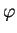

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления