Задача
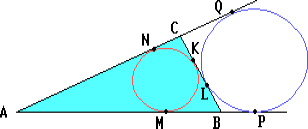
Вписанная окружность треугольника ABC касается стороны BC в точке K, а вневписанная — в точке L. Докажите, что CK = BL = ${\frac{a+b-c}{2}}$, где a, b, c — длины сторон соответственно BC, AC и AB треугольника ABC.
Решение
Пусть M и N — точки касания вписанной окружности со сторонами AB и AC соответственно. Тогда
c = BM + AM = BK + AN = a - CK + b - CN = a - CK + b - CK.
ПоэтомуCK=${\frac{a+b-c}{2}}$.
С другой стороны, если P и Q — точки касания вневписанной
окружности с продолжением сторон AB и AC соответственно, то
BP + CQ = BL + CL = BC = a.
Поэтому
AP = AQ = $\displaystyle {\frac{a+b+c}{2}}$, BL = BP = AP - AB = $\displaystyle {\frac{a+b+c}{2}}$ - c = $\displaystyle {\frac{a+b-c}{2}}$.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет