Задача
Докажите, что во всяком описанном четырёхугольнике середины диагоналей и центр вписанной окружности расположены на одной прямой.
Решение
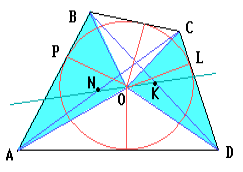
Пусть ABCD – описанный четырёхугольник, O – центр вписанной окружности, r – её радиус, N и K – середины диагоналей AC и BD соответственно.
Если ABCD – ромб, то все эти точки совпадают. В противном случае можно считать, что стороны AB и CD не параллельны.
Заметим, что SANB + SDNC = ½ SABC + ½ SADC = ½ SABCD. Аналогично, SAKB + SDKC = ½ SABCD.
Пусть P и L – точки касания вписанной окружности со сторонами AB и CD. Тогда
SAOB + SCOD = ½ AB·OP + ½ CD·OL = ½ r(AB + CD) = ½ r(AD + BC). Поэтому SAOB + SCOD = ½ SABCD.
Согласно задаче 54571 точки N, O и K лежат на одной прямой.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь