Задача
Четырёхугольник ABCD вписан в окружность; O1, O2, O3, O4 — центры окружностей, вписанных в треугольники ABC, BCD, CDA и DAB. Докажите, что O1O2O3O4 -- прямоугольник.
Решение
Поскольку AO1 и BO1 — биссектрисы треугольника ABC, то
$\displaystyle \angle$AO1B = 90o + $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \angle$ACB.
Аналогично
$\displaystyle \angle$AO4B = 90o + $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \angle$ADB,
а т.к.$\angle$ADB=$\angle$ACB, то$\angle$AO4B=$\angle$AO1B.
Поэтому точкиA,O4,O1иBлежат на одной окружности.
Пусть K — точка на продолжении отрезка BO1 за точку O1.
Тогда
$\displaystyle \angle$O4O1K = 180o - $\displaystyle \angle$O4O1B = $\displaystyle \angle$O4AB = $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \angle$BAD
(т.к. лучAO4— биссектриса углаBAD). Аналогично
$\displaystyle \angle$KO1O2 = 180o - $\displaystyle \angle$O2O1B = $\displaystyle \angle$O2CB = $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \angle$BCD,
а т.к.$\angle$BAD+$\angle$BCD= 180o(противоположные углы вписанного
четырёхугольника), то
$\displaystyle \angle$O4O1O2 = $\displaystyle \angle$O4O1K + $\displaystyle \angle$O2O1K = $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \angle$BAD + $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \angle$BCD = 90o.
Аналогично для остальных углов четырёхугольникаO1O2O3O4.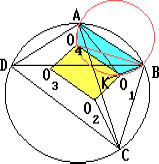
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет