Задача
Высоты треугольника ABC пересекаются в точке H. Докажите, что радиусы окружностей, описанных около треугольников ABC, AHB, BHC и AHC, равны между собой.
Решение
Решение 1:Пусть H1 – точка, симметричная точке H относительно прямой BC. Тогда ∠BH1C = ∠BHC = 180° – ∠A. Поэтому точка H1 лежит на описанной окружности треугольника ABC. Следовательно, описанная окружность треугольника BHC симметрична описанной окружности треугольника ABC относительно прямой BC. Остальное аналогично. 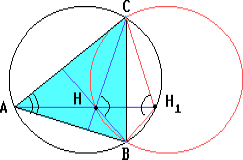
Решение 2:Пусть R и R1 – радиусы описанных окружностей треугольников ABC и BHC соответственно. Тогда
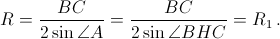
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет