Найдите угол треугольника ABC по условию о высотах — олимпиадная задач
Задача
Расстояние от точки пересечения высот треугольника ABC до вершины C равно радиусу описанной окружности. Найдите угол ACB.
Решение
Пусть H — точка пересечения высот треугольника ABC, C1 — середина AB, O — центр описанной окружности, R — её радиус. Поскольку CH = 2OC1, то
OC1 = $\displaystyle {\textstyle\frac{1}{2}}$СH = $\displaystyle {\textstyle\frac{1}{2}}$R = $\displaystyle {\textstyle\frac{1}{2}}$OA.
Следовательно,
$\displaystyle \angle$AOC1 = 60o, $\displaystyle \angle$AOB = 2$\displaystyle \angle$AOC1 = 120o.
Если точки C и O лежат по одну сторону от прямой AB, то
$\displaystyle \angle$ACB = $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \angle$AOB = $\displaystyle {\textstyle\frac{1}{2}}$ . 120o = 60o.
Если же точкиCиOлежат по разные стороны от прямойAB, то
$\displaystyle \angle$ACB = $\displaystyle {\textstyle\frac{1}{2}}$(360o - $\displaystyle \angle$AOB) = 180o - 60o = 120o.
Расстояние от точки пересечения высот до вершины
треугольника вдвое больше расстояния от центра описанной
окружности до противолежащей стороны.
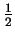
Ответ
60o или 120o.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет