Задача
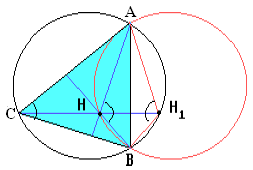
Пусть S — окружность, описанная около треугольника ABC. Докажите, что три окружности, симметричные S относительно прямых, содержащих стороны треугольника, пересекаются в одной точке.
Решение
Пусть H — точка пересечения высот треугольника ABC. Тогда
sin$\displaystyle \angle$AHB = sin$\displaystyle \angle$C.
Поэтому радиус описанной окружности треугольникаAHBравен
радиусу описанной окружности треугольникаABC. Следовательно,
если$\angle$C$\ne$90o, то эти окружности различны и
симметричны относительно прямойAB.
Аналогично для остальных окружностей. Из единственности
окружности, симметричной данной, следует, что три указанные
окружности проходят через точку H.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет