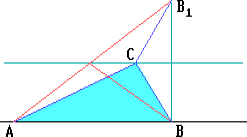
Пусть AB — данное основание треугольника. Тогда геометрическое место точек C, для которых площадь треугольника ABC равна данной, — две прямые, параллельные прямой AB, отстоящие от неё на расстояния, равные высоте треугольника, которая равна удвоенной данной площади треугольника, делённой на данное основание AB.

Пусть l — одна из этих двух прямых. Тогда точка C, для которой периметр треугольника ACB минимален, — точка пересечения прямой l с прямой AB₁, где B₁ — точка, симметричная точке B относительно прямой l. В этом случае треугольник ACB — равнобедренный.

Равнобедренный треугольник.