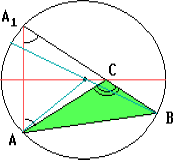
Пусть A₁ — точка, симметричная вершине A относительно биссектрисы внешнего угла C. Тогда

ПосколькуACB— внешний угол равнобедренного треугольникаACA₁, то$\angle$AA₁B=${\frac{1}{2}}$$\angle$ACB. Значит, геометрическое место точекA₁есть дуга фиксированной окружности, проходящей через точкиAиB, расположенная в по ту же сторону от прямойAB, что и точкаC, причём угловая величина этой дуги равна угловой величине данного углаACB Отрезок BA₁ максимален, если BA₁ — диаметр окружности. Тогда точка C — центр этой окружности. Следовательно, CA = CB.

Равнобедренный треугольник.