Задача
Одна из диагоналей вписанного в окружность четырёхугольника является диаметром.
Докажите, что проекции противоположных сторон на другую диагональ равны.
Решение
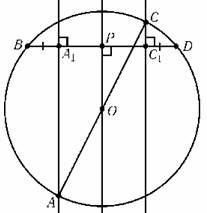
Пусть AC – диаметр окружности, описанной около четырёхугольника ABCD. Опустим перпендикуляры AA1 и CC1 и OP на BD (O – центр описанной окружности; см. рис.). Ясно, что P – середина отрезка BD. Прямые AA1, OP, CC1 параллельны и AO = OC, поэтому A1P = PC1. Так как P – середина BD, то BA1 = DC1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет