Задача
На сторонах произвольного треугольника ABC внешним образом построены равнобедренные треугольники с углами 2α, 2β и 2γ при вершинах A', B' и C', причём α + β + γ = 180°. Докажите, что углы треугольника A'B'C' равны α, β и γ.
Решение
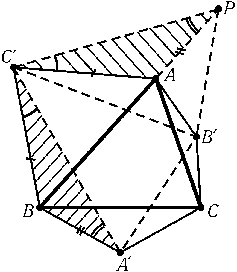
Заметим сначала, что сумма углов при вершинах A, B и C шестиугольника AB'CA'BC' равна 360°, так как по условию сумма его углов при остальных вершинах равна 360°. Построим на стороне AC' внешним образом треугольник AC'P, равный треугольнику BC'A' (см. рис.). Тогда треугольники AB'P и CB'A' равны, так как AB' = CB', AP = CA' и ∠PAB' = 360° – ∠PAC' – ∠C'AB' = 360° – ∠A'BC' – ∠C'AB' = ∠A'CB'. Следовательно, треугольники C'B'A' и C'B'P равны, а значит, 2∠A'B'C' = ∠PB'A' = ∠AB'C, так как ∠PB'A = ∠A'B'C.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь