Задача
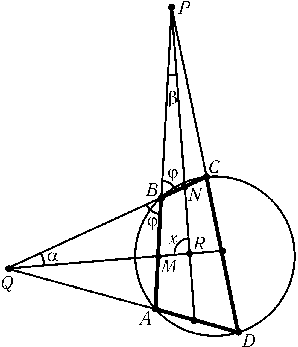
Продолжения сторон ABи CDвписанного четырехугольника ABCDпересекаются в точке P, а продолжения сторон BCи AD — в точке Q. Докажите, что точки пересечения биссектрис углов AQBи BPCсо сторонами четырехугольника являются вершинами ромба.
Решение
Обозначим точки пересечения и углы так, как показано на рис. Достаточно проверить, что x= 90o. Углы четырехугольника BMRNравны 180o-$\varphi$,$\alpha$+$\varphi$,$\beta$+$\varphi$и x, поэтому равенство x= 90oэквивалентно равенству (2$\alpha$+$\varphi$) + (2$\beta$+$\varphi$) = 180o. Остается заметить, что 2$\alpha$+$\varphi$=$\angle$BADи 2$\beta$+$\varphi$=$\angle$BCD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет