О шестиугольнике в треугольнике — олимпиадная задача по планиметрии

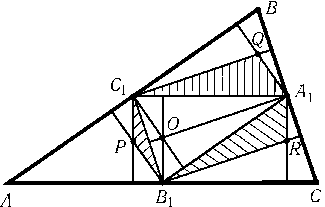
Пусть A₁,B₁и C₁ — середины сторон BC,CAи ABтреугольника ABC. Проведенные отрезки являются высотами треугольников AB₁C₁,A₁BC₁и A₁B₁C. Пусть P,Qи R — точки пересечения высот этих треугольников, а O — точка пересечения высот треугольника A₁B₁C₁(рис.). Рассматриваемый шестиугольник состоит из треугольника A₁B₁C₁и треугольников B₁C₁P,C₁A₁Qи A₁B₁R. Ясно, что$\triangle$B₁C₁P=$\triangle$C₁B₁O,$\triangle$C₁A₁Q=$\triangle$A₁C₁Oи $\triangle$A₁B₁R=$\triangle$B₁A₁O. Поэтому площадь рассматриваемого шестиугольника равна удвоенной площади треугольника A₁B₁C₁. Остается заметить, что S_ABC= 4S_A1B1C1.

Ответ задачи отсутствует