Олимпиадная задача по геометрии: площадь двенадцатиугольника и квадрат
Задача
а) Четыре вершины правильного двенадцатиугольника расположены в серединах сторон квадрата (рис.). Докажите, что площадь заштрихованной части в 12 раз меньше площади двенадцатиугольника. б) Докажите, что площадь двенадцатиугольника, вписанного в окружность радиуса 1, равна 3.
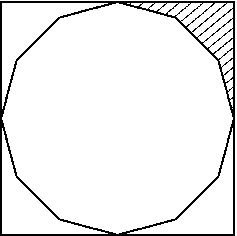
Решение
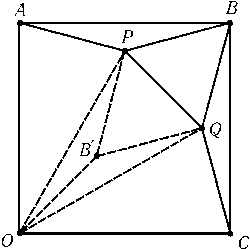
а) Разрежем исходный квадрат на четыре квадрата и рассмотрим один из них (рис.). Пусть точка B'симметрична точке Bотносительно прямой PQ. Докажем, что $\triangle$APB=$\triangle$OB'P. Треугольник APBравнобедренный, причем угол при его основании равен 15o, поэтому треугольник BPQравносторонний. Следовательно,$\angle$OPB'=$\angle$OPQ-$\angle$B'PQ= 75o- 60o= 15oи$\angle$POB'=$\angle$POQ/2 = 15o. Кроме того, AB=OP. Аналогично доказывается, что $\triangle$BQC=$\triangle$OB'Q. Следовательно, площадь заштрихованной на рис. части равна площади треугольника OPQ. б) Пусть площадь правильного двенадцатиугольника, вписанного в окружность радиуса 1, равна 12x. Согласно задаче а) площадь квадрата, описанного около этой окружности, равна 12x+ 4x= 16x; с другой стороны, площадь этого квадрата равна 4, поэтому x= 1/4 и 12x= 3.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь